Comparison between CBOW and Skip-gram

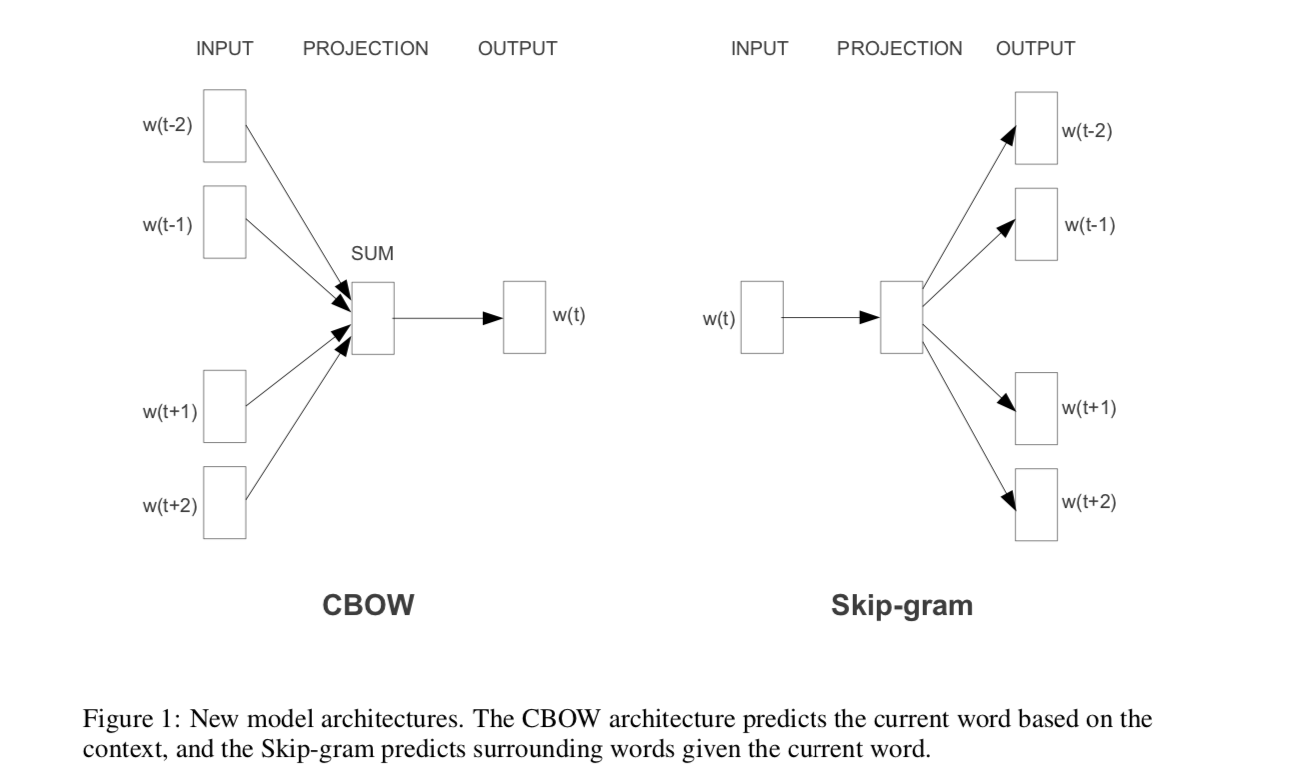
The major difference is that skip-gram is better for infrequent words than CBOW in word2vec. For simplicity, suppose there is a sentence “$w_1w_2w_3w_4$”, and the window size is $1$.

For CBOW, it learns to predict the word given a context, or to maximize the following probability

$$ p(w_2|w_1,w_3) \cdot P(w_3|w_2,w_4)$$

This is an issue for infrequent words, since they don’t appear very often in a given context. As a result, the model will assign them a low probabilities.

For Skip-gram, it learns to predict the context given a word, or to maximize the following probability

$$ P(w_2|w_1) \cdot P(w_1|w_2) \cdot P(w_3|w_2) \cdot P(w_2|w_3) \cdot P(w_4|w_3) \cdot P(w_3|w_4)$$

In this case, two words (one infrequent and the other frequent) are treated the same. Both are treated as word AND context observations. Hence, the model will learn to understand even rare words.

Skip-gram

Main idea of Skip-gram

  • Goal: The Skip-gram model aims to learn continuous feature representations for words by optimizing a neighborhood preserving likelihood objective.

  • Assumption: The Skip-gram objective is based on the distributional hypothesis which states that words in similar contexts tend to have similar meanings. That is, similar words tend to appear in similar word neighborhoods.

  • Algorithm: It scans over the words of a document, and for every word it aims to embed it such that the word’s features can predict nearby words (i.e., words inside some context window). The word feature representations are learned by optmizing the likelihood objective using SGD with negative sampling.

Skip-gram model formulation

Skip-gram learns to predict the context given a word by optimizing the likelihood objective. Suppose now we have a sentence

$$\text{“I am writing a summary for NLP."}$$

and the model is trying to predict context words given a target word “summary” with window size $2$:

$$ \text {I am [ ] [ ] summary [ ] [ ] . }$$

Then the model tries to optimize the likelihood

$$ P(\text{“writing”}|\text{“summary”}) \cdot P(\text{“a”}|\text{“summary”}) \cdot P(\text{“for”}|\text{“summary”}) \cdot P(\text{“NLP”}|\text{“summary”})$$

In fact, given a sentence, Skip-gram is going to, in turn, treat every word as a target word and predict context words. So the objective function is

$$\mathop{\rm argmax} , P(\text{“am”}|\text{“I”}) \cdot P(\text{“writing”}|\text{“I”}) \cdot P(\text{“I”}|\text{“am”}) , … , P(\text{“for”}|\text{“NLP”})$$

To put it in a formal way: given a corpus of words $w$ and their contexts $c$, we consider the conditional probabilities $p(c|w)$, and given a corpus $\text{text}$, the goal is to set the parameters $\theta$ of $p(c|w; \theta)$ so as to maximize the corpus probability:

$$\mathop{\rm argmax}\limits_{\theta} , \prod_{w ,\in ,\text{text}} \prod_{c ,\in ,\text{context($w$)}} p(c|w;\theta) \tag{1}$$

Alternatively, we can write it as

$$\mathop{\rm argmax}\limits_{\theta} , \prod_{(w,c),\in, D} p(c|w;\theta) \tag{2}$$

where $D$ is the set of all word and context pairs we extract from the text. Now we rewrite the objective by taking the $\log$:

$$\mathop{\rm argmax}\limits_{\theta} , \sum_{(w,c),\in, D} \log p(c|w;\theta) \tag{3}$$

The follow-up question comes immediately: how to define the term $p(c|w;\theta)$? It must satisfy the following two conditions:

  • $0 \le p(c|w;\theta) \le 1$;

  • $\sum_{c , \in , \text{context(w)} } \log p(c|w;\theta) = 1$

A natural way is to use the softmax function, so we define it to be

$$ p(c|w;\theta) = \frac{e^{u_c \cdot v_w}}{\sum_{c' , \in , U}e^{u_{c'} \cdot v_w}} \tag{4}$$

where $v_w, u_c \in \mathbb{R}^k$ are vector representations for $w$ and $c$ respectively, and $U$ is the set of all available contexts. Throughout this post, we assume that the target words and the contexts come from distinct vocabulary matrices $V$ and $U$ respectively, so that, for example, the vector associated with the word lunch will be different from the vector associated with the context lunch. One motivation is that every word plays two rules in the model, one as a target word and one as a context word. That’s why we need two separate matrices $U$ and $V$. Note that they must have the same dimension $|\text{Vocab}| \times k$, where $k$ is a hyperparameter and is the dimension of each word vector representation. We would like to set the parameters $\theta$ such that the objective function $(3)$ is maximized.

Here, we use the inner product to measure the similarity between two vectors $v_w$ and $u_c$. If they have a similar meaning, meaning they should have similar vector representation, then $p(c|w;\theta)$ should be assigned for a high probability.

(Side note: Comparison of cosine similarity and inner product as distance metrics – Cosine similarity only cares about angle difference, while dot product cares about angle and magnitude. If you normalize your data to have the same magnitude, the two are indistinguishable.)

By plugging in our definition of $p(c|w;\theta)$, we can write the objective function as

在这里插入图片描述

While the objective can be computed, it is computationally expensive to do so, because the term $p(c|w;\theta)$ is very expensive to compute due to the summation

$$\log (\sum_{c' \in U}e^{u_{c'} \cdot v_w})$$

over all the contexts $c'$ (there can be hundreds of thousands of them). The time complexity is $O(|\text{Vocab}|)$.

Why prefer taking log inside the sum rather than outside

Note: Usually we prefer having the $\log$ inside the sum rather than outside. The log and the sum are part of a function that you want to optimize. That means that, at some point, you will be looking to set the gradient of that function to $0$. The derivative is a linear operator, so when you have the sum of the log, the derivative of the sum is a sum of derivatives. By contrast, the derivative of the log of the sum will have, as seen via the chain rule, a form like $1/\text{(your sum)} \cdot \text{(derivative of the sum)}$. Finding zeros of this function will likely be a much more challenging task, especially if done analytically. On the other hand, since the summation is computational expensive, $\log$ outside the sum often requires technique of approximation, such as using Jensen’s Inequality. Check out my post to know more about Jensen’s inequality.

Now, it’s time to re-formulate the objective function and try to approximate it!

Negative Sampling – Skip-gram model RE-formulation

In our previous Skip-gram model formulation, we assume that if $(w,c)$ is a word and context pair in the training data, then the probability $p(c|w,\theta)$ should be high. Now we can think about this backward and ask: if we have a high (low) probability $p(c|w,\theta)$, is $(w,c)$ really (not) a word and context pair in the training data? In this way of thinking, we formulate a binary classification problem.

Let $p(D=1|w,c)$ be the probability that the pair $(w,c)$ comes from the corpus and $p(D=0|w,c) = 1 - p(D=1|w,c)$ be the probability that the pair $(w,c)$ is not from the corpus.

As before, assume there are parameters $\theta$ controlling the distribution: $p(D = 1|w,c;\theta)$. Since it’s a binary classification problem, we can define it using sigmoid function

$$ p(D=1| w,c;\theta) = \frac{1}{1 + exp(-u_c \cdot v_w)} = \sigma {(u_c \cdot v_w)}$$

Our goal is now finding parameters to maximize the following objective function:

在这里插入图片描述

where the set $\tilde D$ consists of random $(w,c)$ pairs not in $D$. We call a pair $(w,c)$ not in the corpus a negative sample (the name negative-sampling stems from the set $\tilde D$ of randomly sampled negative examples). There are a few points worth mentioning:

  • $1 - \sigma (x) = \sigma (-x)$

  • This objective function looks quite similar to the objective function of logistic regression.

  • In this formulation, we successfully avoid having the $\log$ outside the sum.

Usually, $|D| « |\tilde D|$, so we only pick $k$ negative samples for each data sample. From the original paper, the author suggested that values of $k$ in the range $5$-$20$ are useful for small training datasets, while for large datasets the $k$ can be as small as $2$–$5$.

So if we choose k negative samples for each data sample and denote these negative samples by $N(w)$, then out objective function becomes

$$ L(\theta) = \mathop{\rm argmax}\limits_{\theta} \sum_{(w,c) ,\in,D } \left[\log \sigma(u_w \cdot v_c) + \sum_{c' \in N(w)} \log \sigma (-u_w \cdot v_{c'}) \right] \tag 5$$

SGD for Skip-gram objective function

在这里插入图片描述

Conclusion

Let’s end the topic of Skip-gram model with some details of code implementation:

  • Dynamic window size: the window size that is being used is dynamic – the parameter $k$ denotes the maximal window size. For each word in the corpus, a window size $k′$ is sampled uniformly from $1, . . . , k$.

  • Effect of subsampling and rare-word pruning: words appearing less than min-count times are not considered as either words or contexts, and frequent words (as defined by the sample parameter) are down-sampled. Importantly, these words are removed from the text before generating the contexts. This has the effect of increasing the effective window size for certain words. The motivation for sub-sampling is that frequent words are less informative.

reference: