Authors: Chelsea Finn, Pieter Abbeel, Sergey Levine
Paper reference: https://arxiv.org/pdf/1703.03400.pdf
Contribution
The goal of meta-learning is to train a model on a variety of learning tasks, such that it can quickly solve new learning tasks using only a small number of training samples.
This paper proposes a Model-Agnostic Meta-Learning algorithm (MAML). The key idea underlying the proposed method is to train the model’s initial parameters such that the model has optimal performance on a new task after the parameters have been updated through one or more gradient steps computed with a small amount of data from that new task. There is no assumptions on the form of the model, but it requires that model parameters are smooth enough and can be updated through gradient descent.
Details
Meta-Learning
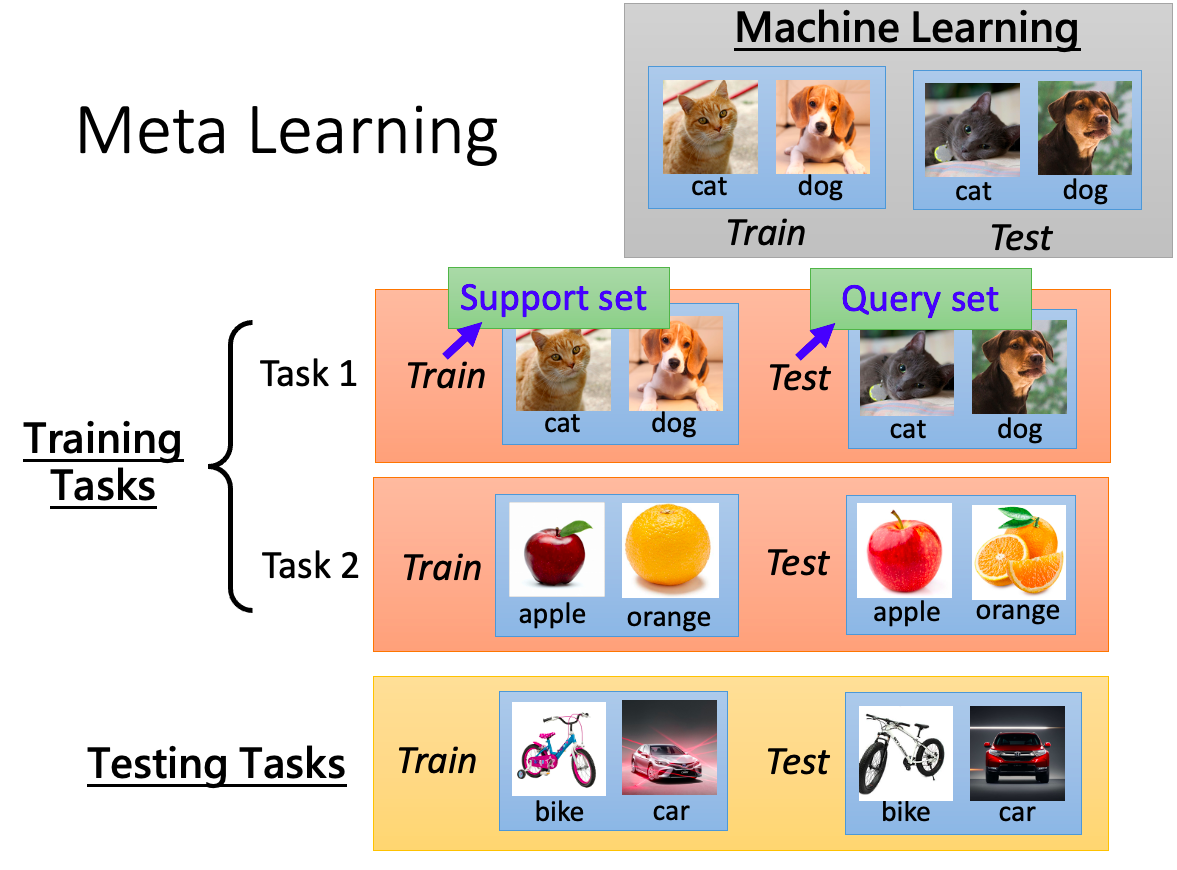
Meta-learning is also known as “learning to learn” and widely considered in few-shot learning. Meta-learning treats tasks as training examples and aasumes that the training tasks and the new task to be solved are from the same distribution. To solve a new task, we first collect lots of tasks, treating each as a training example and train a model to adapt to all those training tasks, finally this model is expected to work well for the new task.
Since the new task only has $k$ labeled examples (few shot), each training task also keeps only $k$ labeled examples during the training. This is to make sure that the training examples (means those training tasks here) have the same distribution as the test example (means the new task here).
Model-Agnostic Meta-Learning algorithm (MAML)

Suppose we have the following:
(1) A learning algorithm $f_{\theta}$ with randomly initialized parameters $\theta$.
(2) A set of training tasks $\mathcal{T}$. Each $\mathcal{T}_i$ is a $N$-way $k$-shot task, where the total number of classes are greater than $N$. Each task $\mathcal{T}i$ contains a support set and a query set (train set and test set) with $k$ and $q$ randomly sampled examples, respectively.
(3) A testing/new task $\mathcal{T}{\text{test}}$ having a support set with $k$ examples and a query set.
The goal is to find parameters $\theta_{\text{final}}$ such that the learning algorithm has optimal performance on a new task after the parameters $\theta$ have been updated ($\theta \to \theta_{\text{final}}$).
Here are the steps for updating parameter $\theta$ for the learning algorithm $f_{\theta}$, and we can iterate these steps many times. The idea is to let the model learn how to do these tasks and then it learns how to generalize to an unseen task.
(1) We first sample a batch of tasks $\mathcal{T}_{i} \sim p(\mathcal{T})$.
(2) For each task $\mathcal{T}_{i}$, we train normally on the support set using a copied $f_\theta$ and update perameters using gradient descent on the training loss $\mathcal{L}_{\mathcal{T}_i}(f_\theta)$. We call the updated parameters $\theta_i^\prime$.
(3) We calculate the loss on the query set of each task $\mathcal{T}_{i}$ using $f_{\theta_i^\prime}$ and sum them up as the total loss $\mathcal{L} = \sum \mathcal{L}_{\mathcal{T}_i}(f_\theta^\prime)$ for learning algorithm $f_{\theta}$.
(4) Update model $f_{\theta}$ by gradient descent on $\mathcal{L}$ and obtain new $\theta$.
After the training is done, we obtain model $F_{\text{final}}$. Then we train this model on the support set of the testing/new task (this is few-shot learning), and check it’s performance on the query set. $F_{\text{final}}$ should quickly adapted to the new task after few training examples.
Figure reference: https://speech.ee.ntu.edu.tw/~tlkagk/courses/ML_2019/Lecture/Meta1%20(v6).pdf