Authors: Rex Ying, Dylan Bourgeois, Jiaxuan You, Marinka Zitnik, Jure Leskovec
Paper reference: https://arxiv.org/pdf/1903.03894.pdf

Contribution

The paper proposes GNNEXPLAINER, a model-agnostic approach for providing interpretable explanations for predictions of any GNN-based model on any graph-based machine learning task.

Specifically, given an instance, GNNEXPLAINER identifies (1) a compact subgraph structure that maximizes the mutual information with GNN’s prediction and (2) a small subset of node features that have a crucial role in GNN’s prediction. Further, GNNEXPLAINER can generate consistent and concise explanations for an entire class of instances.

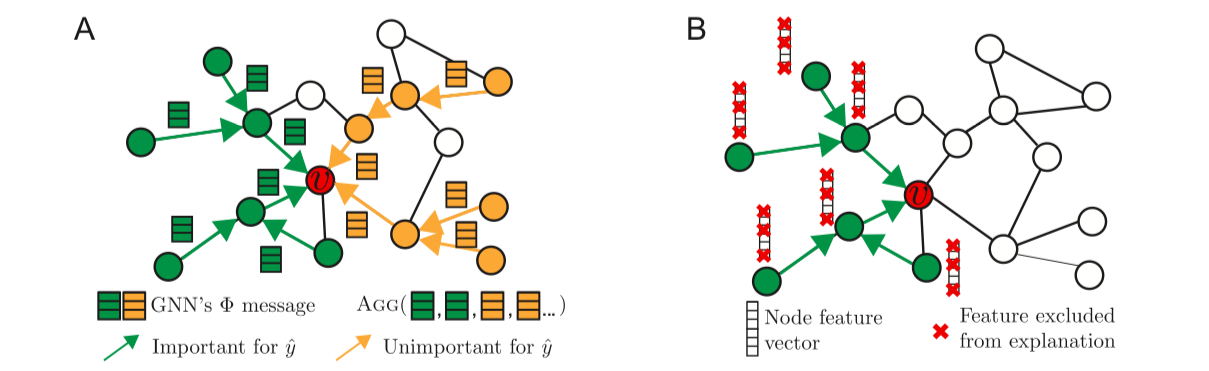
Details

GNNEXPLAINER provides explanations for any GNN that can be formulated in terms of (1) message passing; (2) feature aggregation; (3) parameters update computations.

Single-instance explanations

Given a node $v$, the goal is to identify a subgraph $G_{S} \subseteq G_{c}$ and the associated features $X_{S} = \{ x_{j} \mid v_{j} \in G_{S} \}$ that are important for the GNN’s prediction $\hat{y}$. The notion of importance is denoted by mutual information MI and formulate the GNNEXPLAINER as the following optimization framework:

$$ \max_{G_{S}} M I\left(Y,\left(G_{S}, X_{S}\right)\right)=H(Y)-H\left(Y \mid G=G_{S}, X=X_{S}\right) $$

With a few approximation steps, it can be reformulated as

$$ \min_{\mathcal{G}} H\left(Y \mid G=\mathbb{E}_{\mathcal{G}}\left[G_{S}\right], X=X_{S}\right) $$

Node feature selection

The paper introduces a learnable feature mask F and reparametrize X as a function of F: $$X=Z+\left(X_{S}-Z\right) \odot F$$ s.t. $\sum_{j} F_{j} \leq K_{F}$, where $Z$ is a $d$-dimensional random variable sampled from the empirical distribution and $K_{F}$ is a parameter representing the maximum number of features to be kept in the explanation.

Multi-instance explanations

To obtain a global explanation of class $c$, the rough idea is to covert muiti-instance explanations to single-instance explanation.

Explaination Visualization

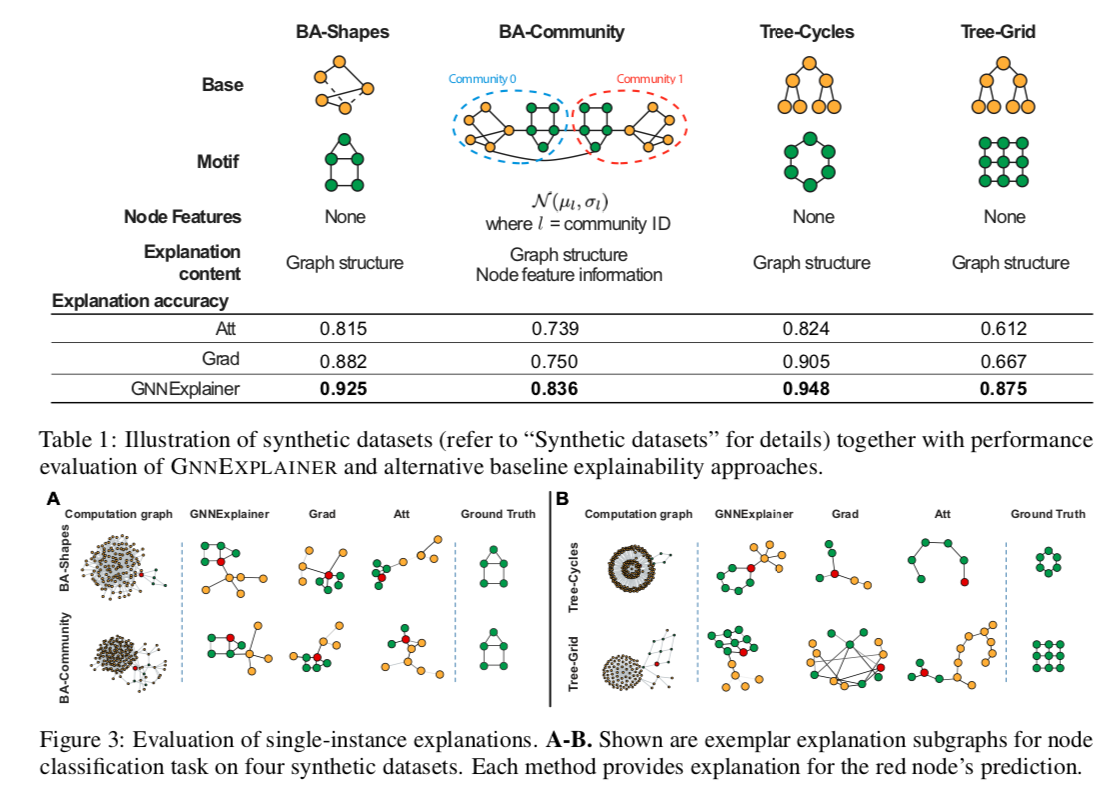
GRAD: a gradient-based method, which computes gradient of the GNN’s loss function with respect to the adjacency matrix and the associated node features.

ATT: a graph attention GNN (GAT) that learns attention weights for edges in the computation graph.