Authors: Soumya Sanyal, Xiang Ren
Paper reference: https://arxiv.org/pdf/2108.13654.pdf

Contribution

The paper proposes Discretized Integrated Gradients (DIG), which allows effective attribution along non-linear interpolation paths. Specifically, it monotonically interpolates between the input word embedding and baseline such that the intermediate points are close to real data samples. This would ensure that the interpolated points are more representative of the word embedding distribution, enabling more faithful model gradient computations.

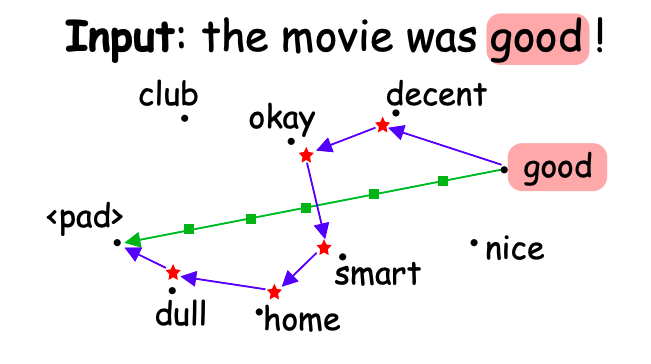
(The blue line, DIG, is a bit misleading…)

Details

Drawbacks of Integrated Gradient (IG)

In IG, the interpolated points are not necessarily representative of the discrete word embedding distribution and can be very far-off from any original word in the embedding space. Using these out-of-distribution intermediate inputs to calculate gradients can lead to sub-optimal attributions.

Discretized Integrated Gradients (DIG)

Procedure

For a given input word embedding,
(1) Find an anchor word. First search for an anchor word (AnchorSearch) from the vocabulary that can be considered as the next interpolation point.
(2) Perturb the anchor word. Since the anchor point need not be monotonic w.r.t. the given input, the paper then optimally perturb the dimensions of the anchor word so that they satisfy the monotonicity constraints (Monotonize, for Riemann summation).
(3) This perturbed point becomes our first interpolation.

For subsequent interpolation points, repeat the above steps using the previous anchor and perturbed points.

Comments

(1) It seems like each time the moved distance between interpolation points $x_i$ and $x_{i+1}$ is varying (based on where the perturbation point is). Is it possible that the first $m-1$ interpolation points are clustered together and far way from the last interpolation point?
(2) After perturbation of anchor words, the remaining embedding is still not “real”. From Table 4, it seems like anchor selection does not make the performance much better.
(3) In Table 4, the DIG-MaxCount method does make the word approximation error low, but its performance is not as good as DIG-Greedy. How that explain the advantage of being close to real word embeddings?