Authors: Chao-Chun Hsu, Chenhao Tan
Paper reference: https://arxiv.org/pdf/2109.06896.pdf
Contribution
This paper proposes a decision-focused summarization which summarizes relevant information for a decision. The goal is to build a summary by selecting representative sentences that lead to similar model (leveraging a predictive model) decisions as using the full text while accounting for textual non-redundancy.
Details
Problem Formulation
Decision-focused summarization task is to identify the most relevant information $\tilde{X}$ from the input $X$ for a particular decision $y$ as a summary in support of human decision making. There also exists a training set analogous to supervised learning (for a predictive model $f$), $D_{train} = \{(X_i , y_i)\}$, which can provide insights on the relation between the text and the decision.
Dataset
A future rating prediction task using Yelp. For each restaurant in Yelp, define $X$ as the text of the first $k=10$ reviews and $y$ is the average rating of the first $t=50$ reviews where $t \gt k$ so that the task is to forecast future ratings. The problem is to select sentences from a restaurant’s first 10 reviews in support of predicting its future rating after 50 reviews.
DecSum
The goal of the approach is to:
(1) develop a model $f$ (Longformer in the paper) to make the decision $y = f(X)$;
(2) build summaries that can support $f$ in decision making and account for properties in text-only summarization.
Decision-focues summaries should satisfy:
(1) Decision Faithfulness. The selected sentences should lead to similar decisions as the full text: $f(\tilde{X}) \simeq f(X)$:
$$
\mathcal{L}_{\mathrm{F}}(\tilde{X}, X, f)=\log |f(\tilde{X})-f(X)|
$$
(2) Decision representativeness. The decision distribution of the summary (selected sentenes) $\hat{Y}_{\tilde{X}}=\{f(x) \mid x \in \tilde{X}\}$ should be close to the decision distribution of all sentences in the full text $\hat{Y}_{X}=\{f(x) \mid x \in X\} .$ The second loss function is the logarithm of the Wasserstein distance: $$ \mathcal{L}_{\mathrm{R}}(\tilde{X}, X, f)=\log \left(W\left(\hat{Y}_{\tilde{X}}, \hat{Y}_{X}\right)\right) $$
(3) Textual non-redundancy. The selected sentences should capture diverse contents and provide an overview of the textual information in the input text: $$ \mathcal{L}_{\mathrm{D}}(\tilde{X})=\sum_{x \in \tilde{X}} \max_{x^{\prime} \in \tilde{X}-{x}} \operatorname{cossim}\left(s(x), s\left(x^{\prime}\right)\right) $$
where the cosine similarity is based on SentBERT sentence representation. The final objective function consists of the above three parts: $$ \mathcal{L}(\tilde{X}, X, f)=\alpha \mathcal{L}_{\mathrm{F}}(\tilde{X}, X, f)+\beta \mathcal{L}_{\mathrm{R}}(\tilde{X}, X, f)+\gamma \mathcal{L}_{\mathrm{D}}(\tilde{X}), $$ where $\alpha, \beta, \gamma$ control the tradeoff between the three desiderata.
Implementation
Greedily selects a sentence (with beam search) that minimizes the loss function.
Results
The paper considers servral baselines to extract partial inputs as explanation:
- Text-only summarization baselines such as PreSumm (an extractive summarization method), BERT, randomly select sents;
- Attribution methods such as IG, attention to rank and select sentences.
Experiments show that baselines are not faithful ($\log |f(\tilde{X})-f(X)|$ is big)
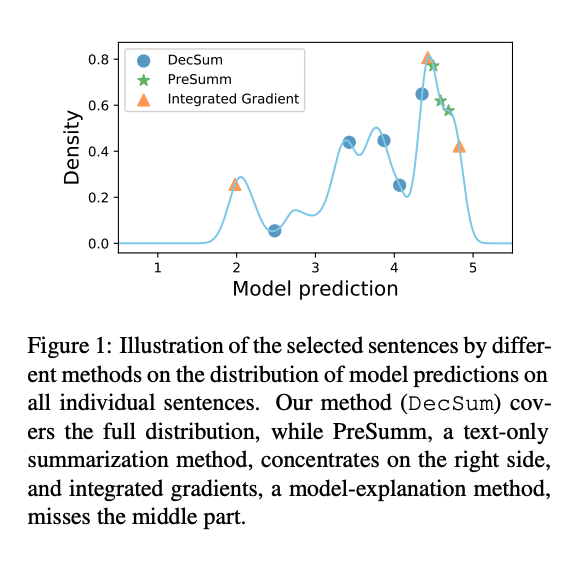
Footnote: The distance between $\hat{Y}_{\tilde{X}}$ and $\hat{Y}_{X}$ is measured by Wasserstein Distance: $$W(\hat{Y}_{\tilde{X}}, \hat{Y}_{X})=\inf_{\gamma \in \Gamma\left(\hat{Y}_{\tilde{X}}, \hat{Y}_{X}\right)} \int_{\mathbb{R} \times \mathbb{R}} | f-f^{\prime}|| d \gamma\left(f, f^{\prime}\right),$$ where $\Gamma (\hat{Y}_{\tilde{X}}, \hat{Y}_{X})$ denotes the collection of all measures on $\mathbb{R} \times \mathbb{R}$ with marginals $\hat{Y}_{\tilde{X}}$ and $\hat{Y}_{X}$ on the first and second factors respectively.